Você sabia que geometria é um dos assuntos mais cobrados na parte de Matemática e suas Tecnologias da prova do Enem? Em especial, questões que exijam o cálculo dos volumes de sólidos são recorrentes (veja os outros assuntos mais recorrentes aqui). Aprenda a calcular o volume dos sólidos geométricos:
Volume dos prismas
Os primas podem ser definidos como sólidos geométricos delimitados por faces planas e que possuem duas bases, superior e inferior, as mesmas formas e dimensões em planos paralelos e congruentes.
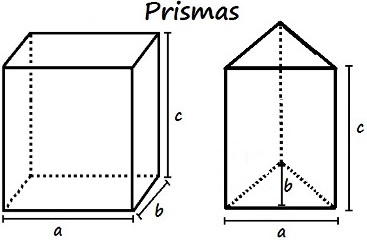
Os volumes dos prismas irão depender sempre do formato da base e devem ser calculados de acordo com a seguinte formula:
Volume = (área da base) . altura
No paralelepípedo acima, calcularemos o volume deste prisma da seguinte forma:
V = a . b . c
Já o volume do prisma de base triangular:
V = a . b . c
2
* Lembrando que a área de um triangulo equilátero é calculada da seguinte forma:
área da base x altura / 2
Volume dos cilindros
.jpg)
Para o cálculo dos volumes dos cilindros, iremos seguir a mesma lógica do volume dos prismas. Sabendo que a área de uma circunferência é π . r2 , calcularemos o volume de um cilindro da seguinte forma:
V = (área da base) . altura
V = π . r2 . a
Volume de um cone
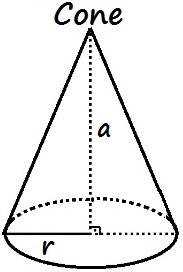
O volume dos cones possuem uma particularidade. Ao invés de multiplicarmos a área da base pela a altura, iremos multiplicar a área da base por 1/3 da altura. Ficando a fórmula de cálculo da seguinte forma:
V = (área da base) . 1/3 altura
O cilindro acima seria calculado da seguinte maneira:
V = π . r2 . a
3
Volume de uma pirâmide
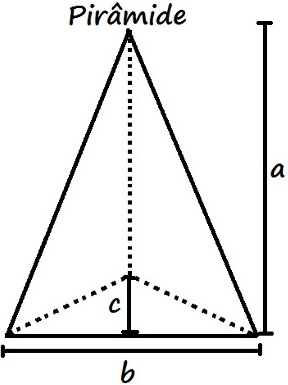
O volume das piramides devem ser calculadas da mesma forma que você aprendeu a calcular o volume dos cones:
V = (área da base) . 1/3 altura
Já sabendo que a área do triangulo equilátero, calcularemos a área da pirâmide acima da seguinte forma:
V = b. c . a
2 3
V = b . c . a
6
Curtiu o post e quer saber mais sobre Matemática para arrasar na prova do Enem? Não deixe de conhecer o curso Matemática do Zero!
Agora com 40% de desconto você pode adquirir as melhores aulas para se preparar por completo para as questões de matemática do Enem, é só clicar aqui para sair na frente com o QG!
