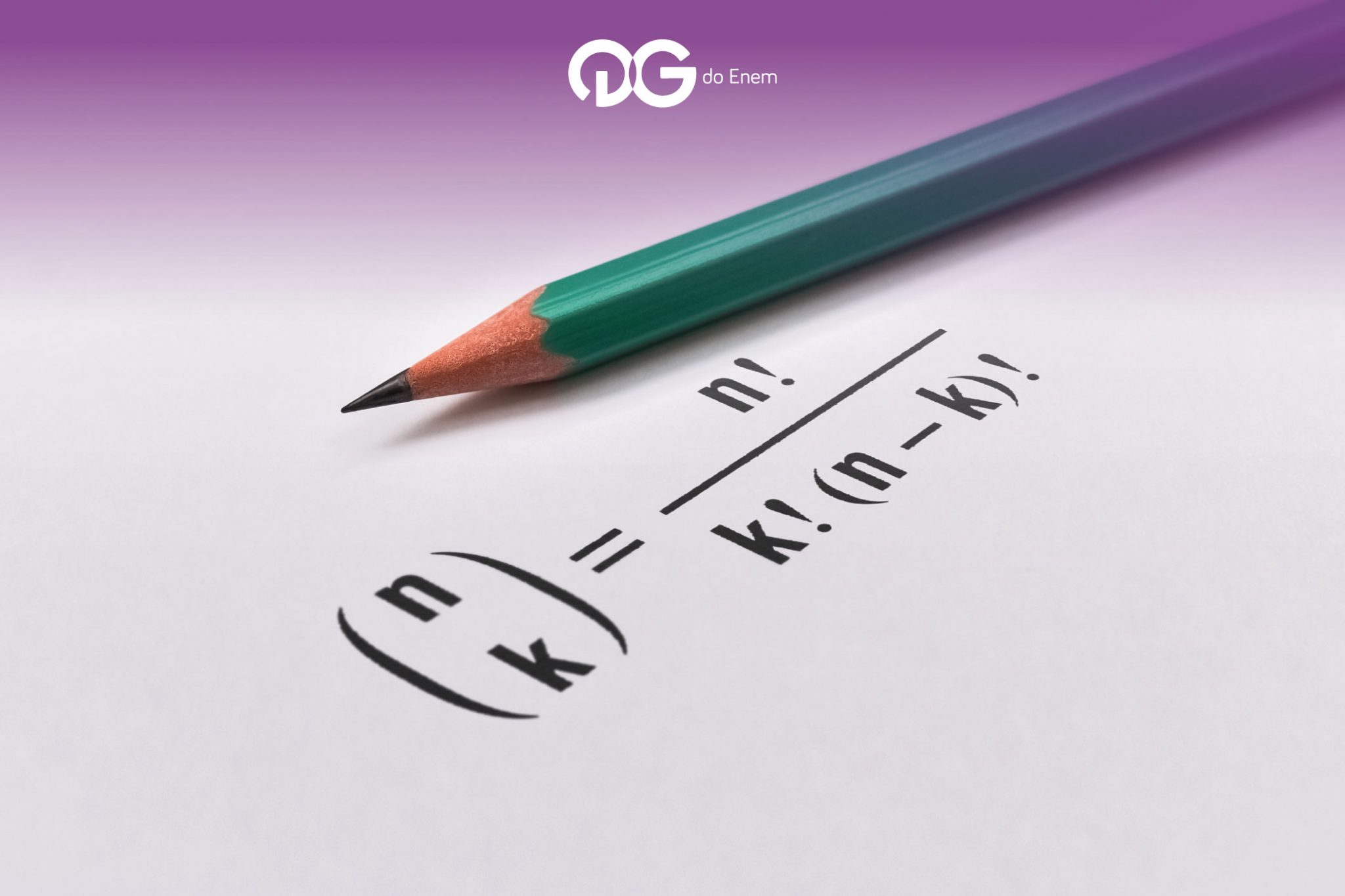De todos os assuntos referentes a área de exatas, Matemática combinatória aparece constantemente em vestibulares. Apesar da frequência nas provas, este assunto matemático sempre amedronta os estudantes. Desse modo, apresentaremos algumas dicas para facilitar esta compreensão.
Primeiramente, é importante ressaltar que grande parte das questões que envolvem combinatória necessitam da interpretação do enunciado. Questões de combinatória sempre seguem um padrão visando calcular contagens em maneiras distintas, utilizando de alguns métodos. Dentro de combinatória, existem dois tipos de princípios: o multiplicativo e o aditivo. O primeiro consiste, como o próprio nome sugere, no produto entre os elementos a serem contados; é representado nos enunciados pela conjunção e. Enquanto o principio aditivo, soma os elementos a serem contados, sendo representado pela conjunção ou.
Dica: ou significa somar, e significa multiplicar

Exemplo: Existem sanduíches de 3 sabores (frango, carne, vegetariano) que podem vir com suco de 3 sabores (laranja, uva, maracujá) também.
Pergunta 1: João quer pedir um sanduíche e um suco, de quantas maneiras diferentes pode chegar o pedido dele?
3(sabores de suco) X 3(sabores de sanduíche) = 9
Pergunta 2: Maria tem a opção de ganhar um suco ou um sanduíche, de quantas maneiras ela poderia obter seu prêmio?
3(sucos) + 3(sanduíches) = 6
Além disso, existem três métodos de matemática combinatória que mais aparecem em vestibulares, sendo eles: permutação, combinação e arranjo. A permutação é utilizada em um conjunto com um certo numero de elementos ordenado podendo ser arranjado em diversas formas diferentes. Este método também pode aparecer com elementos repetidos, esta terá sua forma específica de resolução.
A permutação é representada por Pn = n!, enquanto a mesma com repetição é representada por Pn,k= n!/k!, sendo k o elemento repetido.
Exemplo: Calcular os anagramas da palavra CAFÉ e BANANA
CAFÉ = 4 letras
4! = 4x3x2x1 = 24.
ou seja, a palavra café pode ser ordenada de 24 formas diferentes
BANANA = 6 letras, 2 repetições
6!/3!2! = 6x5x4x3!/3!2×1 = 120/2 = 60
a palavra banana pode ser ordenada de 60 formas diferentes
Dentre os três métodos, o segundo é a combinação, que consiste em um subconjunto onde a ordem não importa. Combinação tem uma fórmula específica onde C(n,p) = n!/p!(n-p)!, onde n é o total de elementos e p o numero de elementos escolhido.
Por outro lado, o Arranjo, terceiro método de combinatória, segue os mesmos moldes da combinação, com exceção de uma regra: a ordem importa. A formula do Arranjo consiste em A(n,p) = n!/(n-p)!.
Dica: É sempre importante deixar claro se a ordem importa ou não, “perguntando” para o enunciado.
Exemplo: De 10 candidatos à diretoria de um clube, apenas 2 serão escolhidos para ocupar os cargos.
Pergunta 1: De quantas maneiras diferentes, os cargos poderão ser preenchidos?
Aqui a ordem não importa, então usaremos combinação
C(10,2) = 10!/2!8!= 45 formas diferentes
Pergunta 2: De quantas maneiras diferentes, os cargos poderão ser preenchidos sabendo que o mais votado terá o cargo de presidente e o vice de diretor?
Aqui a ordem importa, pois se P1 e P2 forem os mais votados, P1 será presidente e P2 será diretor; Porém,o inverso não é equivalente, isto é: P2 seria presidente e P1 seria diretor.
Dessa forma, usaremos arranjo
A(10,2) = 10!/8! = 90 casos distintos.
A matemática combinatória é um assunto que também pode ser enquadrado em outras áreas, como probabilidade e computação. É sempre bom que os alunos pratiquem este tipo de conteúdo para fixar o conhecimento e arrasar nos vestibulares!
Gostou do texto? clique aqui para ver mais conteúdo como este e veja nossos vídeos sobre Combinatória!