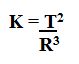No início do séc. XVII, o astrônomo e matemático alemão, Johannes Kepler, teorizou três leis que explicariam o movimento da Terra ao redor do Sol. As leis de Kepler, como ficaram conhecidas, não se aplicam somente aos planetas orbitando o Sol, mas a todos os corpos celestiais que orbitam um outro por influência da gravidade. Veja a explicação das três leis:
Primeira Lei de Kepler
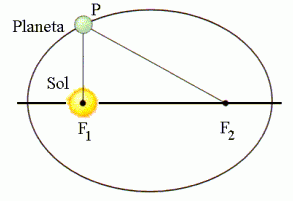
A primeira lei de Kepler, muitas vezes conhecida como a “Lei das órbitas”, descreve que as órbitas dos planetas ao redor do Sol possuem um modelo orbital elíptico e não circular, como se pensava antes. Uma elipse pode ser definida como uma figura geométrica curvilínea em que a soma das distâncias de qualquer ponto da curva até dois pontos fixos (chamados de focos) resulta uma constante.
Segunda Lei de Kepler
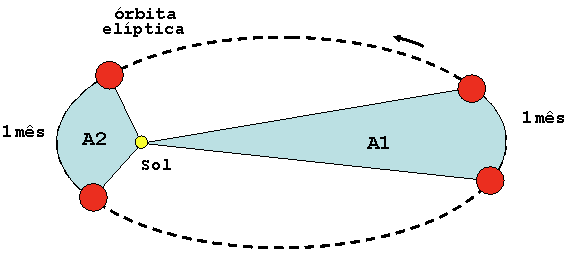
Também conhecida como a “Lei das áreas”, explica que as velocidades dos planetas em suas órbitas não são constantes e variam de acordo com a distância que o corpo celeste está do sol. Nesta lógica, Kepler descobriu que um planeta irá se mover mais rápido quando se encontrar em uma posição mais perto do Sol, e mais devagar quando se estiver mais distante.
Além disso, se você imaginar uma linha escrita do centro do nosso planeta até o centro do sol, está linha irá percorrer a mesma área em períodos de tempos iguais durante a órbita. Como é possível ver na imagem a cima.
Terceira Lei de Kepler
Chamada de “Lei dos períodos”, a terceira lei de Kepler descreve a relação entre a distância de cada planeta ao Sol e seu período de translação (movimento que descreve a volta dos planetas em torno do Sol, correspondente ao período dos anos). Diferentemente das outras leis, a terceira lei de Kepler relaciona as características dos movimentos de diferentes planetas com outros.
Kepler descobriu que a razão entre os quadrados dos períodos de translação dos planetas e os cubos dos respectivos raios médios das órbitas será sempre constante. Veja a equação:
Onde:
T: corresponde ao tempo de Translação do planeta
R: o raio médio das órbitas planetares
K: constante que depende da massa do sol
Agora confira uma questão do Enem em que este assunto foi tópico:
( Enem 2009) O ônibus espacial Atlantis foi lançado ao espaço com cinco astronautas a bordo e uma câmera nova, que iria substituir uma outra danificada por um curto-circuito no telescópio Hubble. Depois de entrarem em órbita a 560 km de altura, os astronautas se aproximaram do Hubble. Dois astronautas saíram da Atlantis e se dirigiram ao telescópio. Ao abrir a porta de acesso, um deles exclamou: “Esse telescópio tem a massa grande, mas o peso é pequeno.”
Considerando o texto e as leis de Kepler, pode-se afirmar que a frase dita pelo astronauta:
A) Se justifica porque o tamanho do telescópio determina a sua massa, enquanto seu pequeno peso decorre da falta de ação da aceleração da gravidade.
B) Se justifica ao verificar que a inércia do telescópio é grande comparada à dele próprio, e que o peso do telescópio é pequeno porque a atração gravitacional criada por sua massa era pequena.
C) Não se justifica, porque a avaliação da massa e do peso de objetos em órbita tem por base as leis de Kepler, que não se aplicam a satélites artificiais.
D) Não se justifica, porque a força-peso é a força exercida pela gravidade terrestre, neste caso, sobre o telescópio e é a responsável por manter o próprio telescópio em órbita.
E) Não se justifica, pois a ação da força-peso implica a ação de uma força de reação contrária, que não existe naquele ambiente. A massa do telescópio poderia ser avaliada simplesmente pelo seu volume.
Gabarito: D