A segunda competência da prova de Matemática do Enem (Exame Nacional do Ensino Médio) cobra conteúdos do ensino fundamental como metro quadrado, metro cúbico, pi, raio e teorema de Pitágoras. Além desses conteúdos básicos, é importante fazer uma boa revisão do conteúdo de geometria do ensino médio. Saber o valor de um ângulo, conhecer o poliedro e o prisma e as relações entre os triângulos é uma forma de garantir uns pontos a mais no Enem.
Exemplo 1
Nesta questão, o aluno precisava estar em dia com os conceitos de massa, volume, comprimento e capacidade. Então, vamos relembrar os conceitos:
· massa é a quantidade de matéria contida em um objeto ou corpo.
· volume é o espaço que um corpo ocupa.
· comprimento é distância entre dois pontos.
· capacidade é quanto cabe em um determinado espaço.
Enem 2010
A siderúrgica “Metal Nobre” produz diversos objetos maciços utilizando o ferro. Um tipo especial de peça feita nessa companhia tem o formato de um paralelepípedo retangular, de acordo com
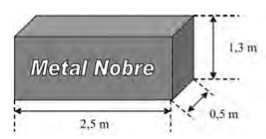
O produto das três dimensões indicadas na peça resultaria na medida da grandeza
a) massa.
b) volume.
c) superfície.
d) capacidade.
e) comprimento.
Resolução: o volume de um paralelepípedo é o produto de suas três dimensões comprimento x largura x altura. Não existe a interpretação de “capacidade” no lugar de “volume”, pois a questão especifica que o sólido é maciço.
Gabarito: b
Exemplo 2
Nesta questão, o aluno precisava demonstrar o conhecimento de congruências e semelhanças entre triângulos.
Enem 2010
Em canteiros de obras de construção civil é comum perceber trabalhadores realizando medidas de comprimento e de ângulos e fazendo demarcações por onde a obra deve começar ou se erguer. Em um desses canteiros foram feitas algumas marcas no chão plano. Foi possível perceber que, das seis estacas colocadas, três eram vértices de um triângulo retângulo e as outras três eram os pontos médios dos lados desse triângulo, foram indicadas por letras.

A região demarcada pelas estacas A, B, M e N deveria ser calçada com concreto.
Nessas condições, a área a ser calçada corresponde
a) à mesma área do triângulo AMC
b) à mesma área do triângulo BNC.
c) à metade da área formada pelo triângulo ABC.
d) ao dobro da área do triângulo MNC.
Resolução: existe uma semelhança entre os triângulos BAC e MNC, K= = 2 e a razão entre suas áreas é igual a k²=4. Portanto, sendo S a área do triangulo MNC e C iguala região que deveria ser calçada com concreto, tem-se: =k² que corresponde a C+S=4S= C+3S, logo a área que deveria ser calçada é o triplo da área do triângulo MNC.
Gabarito: e
Fonte da resolução: Globo Educação
Exemplo 3
Enem 2010
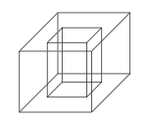
Um porta-lápis de madeira foi construído no formato cúbico, seguindo o modelo ilustrado a seguir. O cubo de dentro é vazio. A aresta do cubo maior mede 12 cm e a do cubo menor, que é interno, mede 8 cm.
O volume de madeira utilizado na confecção desse objeto foi de
a) 12 cm3
b) 64 cm3
c) 96 cm3
d) 1216 cm3
e) 1728 cm3
Resolução: o volume do cubo externo subtraído o volume do cubo interno é igual ao volume de madeira utilizado na confecção desse objeto, logo, tem-se que o volume de madeira utilizado na confecção foi de: 12³-8³= 1216cm³.
Gabarito: d
Fonte da resolução: Globo Educação
Competência de área 2 – Utilizar o conhecimento geométrico para realizar a leitura e a representação da realidade e agir sobre ela.
H6 – Interpretar a localização e a movimentação de pessoas/objetos no espaço tridimensional e sua representação no espaço bidimensional.
H7 – Identificar características de figuras planas ou espaciais.
H8 – Resolver situação-problema que envolva conhecimentos geométricos de espaço e forma.
H9 – Utilizar conhecimentos geométricos de espaço e forma na seleção de argumentos propostos como solução de problemas do cotidiano.