A gente sabe que matemática assusta, mas pode ficar tranquilo que estamos aqui só para te ajudar! Na dica de hoje, o professor Jairo Teixeira te explica o básico da Geometria para você dar um show no ENEM! Vem com o QG!
Antes de começar com conteúdo, deixamos aqui algumas dicas muito importantes para estudar Matemática:
ÂNGULOS
1) DEFINIÇÃO
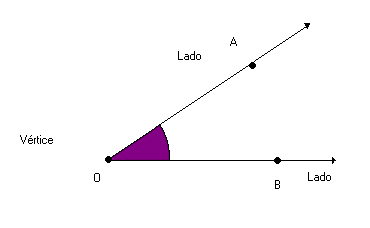
Ângulo é a região de um plano determinada pelo encontro de duas semirretas que possuem uma origem em comum, chamada vértice do ângulo.
Sua abertura é medida em radianos ou graus.
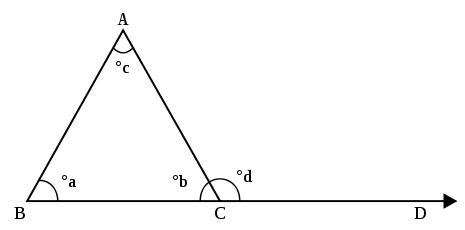
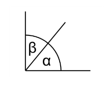
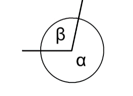
2) ÂNGULO INTERNO E ÂNGULO EXTERNO
3) CLASSIFICAÇÃO DOS ÂNGULOS
De acordo com o valor de sua medida, os ângulos se classificam em:
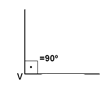
- Ângulo reto: sua medida é igual a 90º.
- Ângulo agudo: sua medida é menor que 90º.
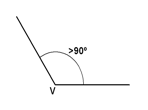
- Ângulo obtuso: sua medida é maior que 90º.
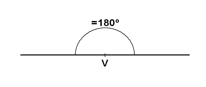
- Ângulo raso: sua medida é igual a 180º.
4) MEDIDA DE UM ÂNGULO
A abertura de um ângulo é medida em graus ou em radiano.
- Grau: Um grau corresponde a 1/360 de uma circunferência.
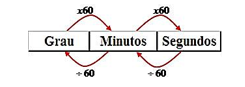
Observação: Submúltiplos do grau
1 grau = 60 minutos
1 minuto = 60 segundos
Exemplo: 42,72º
42o + 0,72o = 42o + 0,72 x 60 = 42o 43,2’
42o 43,2’ = 42o 43’ + 0,2 x 60 = 42o 43’ 12’’
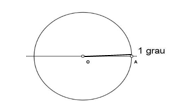
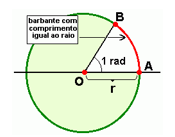
- Radiano: Um radiano corresponde à medida de um ângulo em um círculo, cujo arco tem como comprimento a medida do raio do círculo.
Observação: Uma circunferência completa tem 2p radianos, ou seja:
2p rad = 360o
5) ÂNGULOS COMPLEMENTARES, SUPLEMENTARES E REPLEMENTARES
- Ângulos Complementares: dizemos que dois ângulos são complementares quando a soma de suas medidas é igual a 90º.
Exemplo: 30º e 60º.
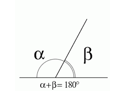
- Ângulos Suplementares: dizemos que dois ângulos são suplementares quando a soma de suas medidas é igual a 180º.Exemplo: 40º e 140º.
- Ângulos Replementares: dizemos que dois ângulos são replementares quando a soma de suas medidas é igual a 360º.
Exemplo: 260º e 100º.
1) DEFINIÇÃO
Ceviana é um segmento de reta que tem uma extremidade em um vértice de um triângulo e a outra na reta suporte do lado oposto. As principais cevianas são mediana, bissetriz e altura.
O encontro das cevianas determinam pontos notáveis de um triângulo.
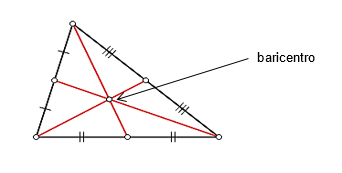
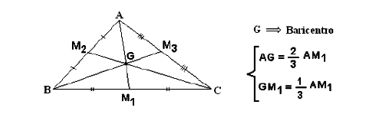
2) MEDIANA
Mediana é o segmento de reta que tem uma extremidade em um vértice de um triângulo e a outra no ponto médio do lado oposto. As medianas se encontram em um ponto chamado baricentro.
Observação: O baricentro divide cada mediana na razão 2/3 a partir do vértice:
3) BISSETRIZ
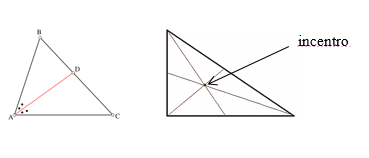
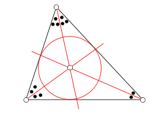
A bissetriz divide um ângulo interno de um triângulo ao meio. Elas se encontram em um ponto chamado incentro.
Observação: o incentro é o centro da circunferência inscrita no triângulo.
4) ALTURA
A altura é o segmento de reta com origem em um dos vértices de um triângulo e perpendicular ao lado oposto. Elas se encontram em um ponto chamado ortocentro.
No triângulo acutângulo o ortocentro é ponto interior do triângulo.
No triângulo retângulo o ortocentro coincide com o vértice do ângulo reto.
No triângulo obtusângulo o ortocentro é ponto exterior ao triângulo.
Observação: Embora a mediatriz e bissetriz externa não sejam cevianas, definem pontos importantes em um triângulo.
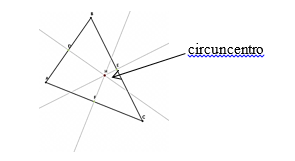
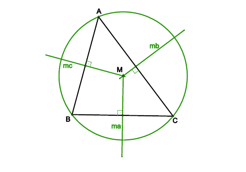
Mediatriz: é uma reta que passa perpendicularmente pelo ponto médio de um segmento. Em um triângulo, cada lado tem sua mediatriz, e elas se encontram em um ponto chamado circuncentro.
O circuncentro é o centro da circunferência circunscrita no triângulo.
No triângulo acutângulo o circuncentro é ponto interior do triângulo.
No triângulo retângulo o circuncentro é ponto médio do maior lado do triângulo (hipotenusa).
No triângulo obtusângulo o circuncentro é ponto exterior ao triângulo.
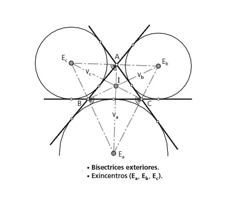
Bissetriz externa: divide o ângulo externo ao meio.
Um exincentro é um ponto de intersecção das bissetrizes externas de um triângulo qualquer. A partir dele, podem ser traçadas circunferências que tangenciam um dos lados e o prolongamento dos outros dois.
Assista à explicação do professor:
Curtiu?! Confira nosso curso de Matemática: http://bit.ly/CursoMatematicaQG