O estudo de funções matemáticas e suas características é bem recorrido dentro das Exatas, a presença deste assunto é constante na maioria dos exames de vestibulares. No ENEM, especificamente, essa matéria correspondeu a 7% do conteúdo do caderno de matemática do exame.
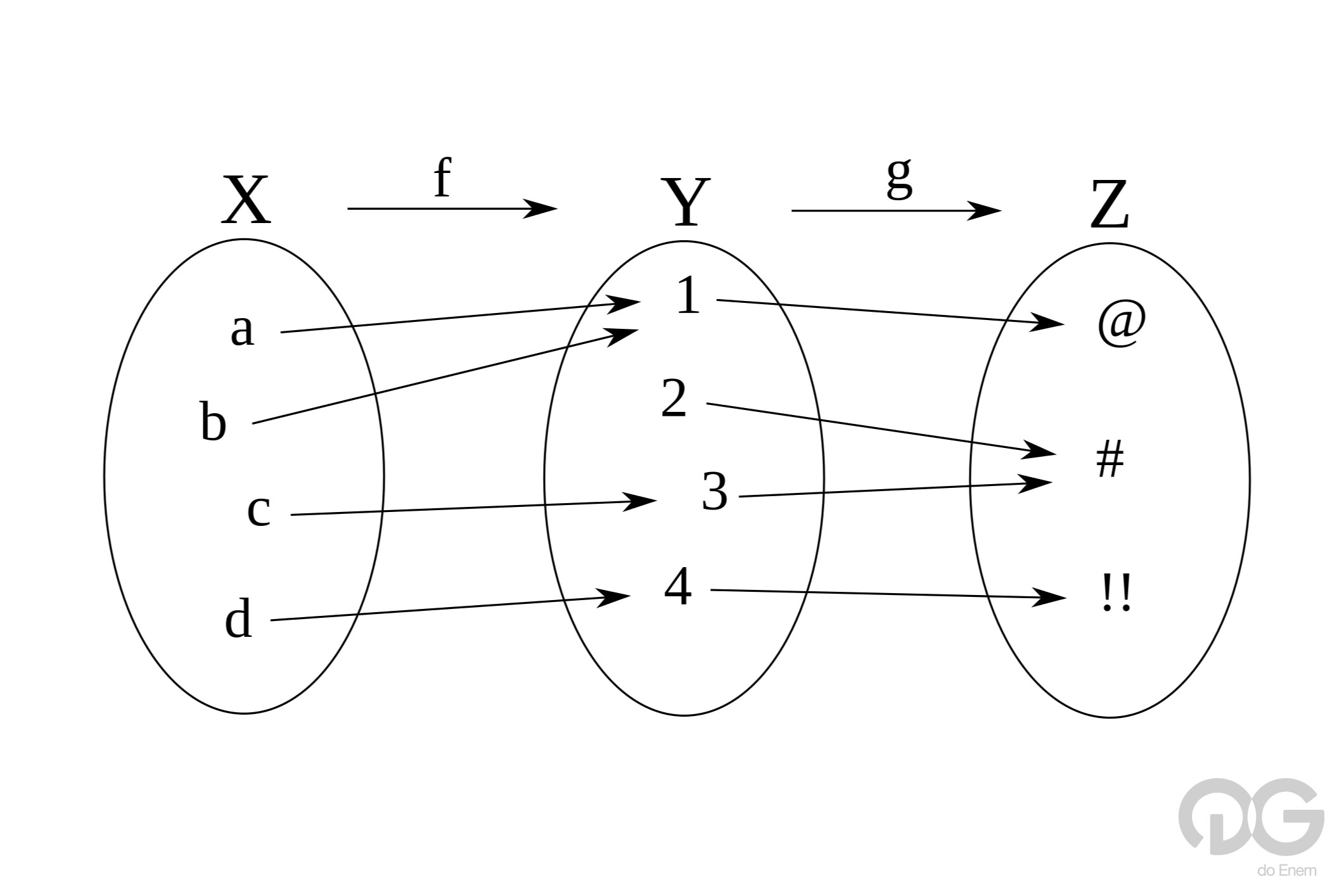
Antes de tudo, é necessário entender o que é uma função matemática. Esta pode ser determinada pela relação entre dois conjuntos com alguma associação. As funções geralmente são escritas como f: A → B ou y = f(x). Onde f representa é o nome da função, A é o domínio e B é o contradomínio.
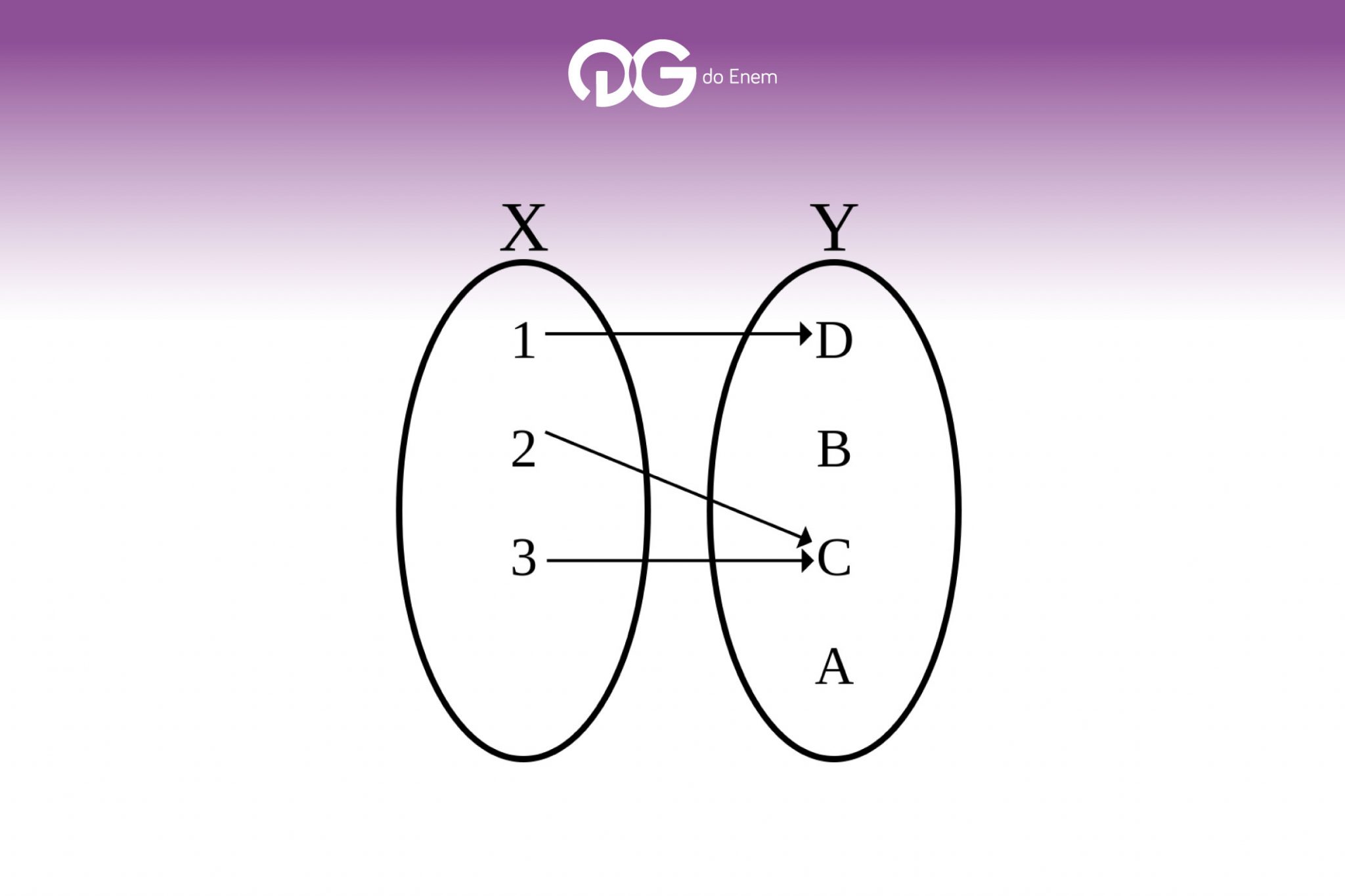
As funções contam com três conjuntos, sendo eles o domínio, imagem e contradomínio.
O domínio é de onde partem as setas, em outras palavras, é no domínio em “saem” os valores para a definição da função. O contradomínio é o conjunto onde chegam as setas que saíram do domínio, porém, nem todos os elementos do contradomínio recebem as setas. A imagem é o conjunto onde os elementos são atingidos pela seta do domínio.
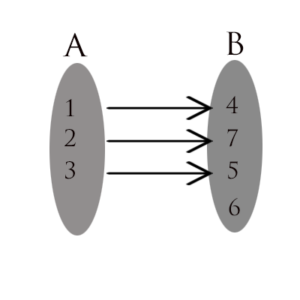
Na imagem abaixo, A representa o domínio, B representa o contradomínio e o conjunto {4,5,7} a imagem da função.
Observação: todos os elementos do domínio devem conter uma e apenas uma flecha indicando a “partida”, nenhum deles deve ficar vazio, senão a relação não será uma função.
Ademais, as funções são caracterizadas por três tipos: injetoras, sobrejetoras e bijetoras.
O primeiro dos tipos, nas injetoras, cada elemento do domínio se associa a um único elemento da imagem. Caso não sobre nenhum elemento no contradomínio, ele será igual a imagem; caso contrário, como mostrado na imagem acima, o contradomínio é diferente da imagem. Logo:
D(f) = {1,2,3}
CD (f) = {4,5,6,7}
Im(f) = {4,5,7}
No segundo tipo, as funções sobrejetoras são exemplificadas como cada elemento do domínio possui um elemento da imagem. Neste caso, um elemento do domínio pode se associar a mais de um elemento da imagem. Por consequência disso, nas funções sobrejetoras a imagem e contradomínio são iguais.
Nesse caso:
D(f) = {1,2,3}
CD(f) = {4,5,6,7}
Im(f) = {4,5,6,7}

Por último, as funções bijetoras são injetoras e sobrejetoras ao mesmo tempo. Ou seja, cada elemento do domínio será associado uma única vez a um elemento da imagem e a imagem e o contradomínio possuem os mesmos elementos.
De acordo com o exemplo:
D(f) = {1,2,3}
CD(f) = {4,5,7}
Im(f) = {4,5,7}
Funções matemáticas aparecem no ENEM muitas vezes por meio de contextualizações, mas que é fundamental ter essa base teórica sobre o assunto. No canal do youtube do QG do ENEM, você encontrará uma aula mais aprofundada sobre o assunto (clique aqui).